physicsa.com
class code: SPS21 teacher: Mr. Elert
classroom: n/a office: n/a
test day: unknown phone: n/a
office hours: n/a email: n/a

Physics A: Problem Set 15: The nature of light

recommended reading

High Marks: n/a
Barron's Let's Review: 12.1–12.4
physics.info: The nature of light
Wikipedia: Light, Speed of light, Visible spectrum
HyperPhysics: Speed of light, Visible light
Khan Academy: Introduction to light waves
YouTube: Roy G. Biv
Mr. Machado: 15 Wave Phenomena - From Sound to Light
Reference table with select items highlighted, page 1 Reference table with select items highlighted, page 2 Reference table with select items highlighted, page 3 Reference table with select items highlighted, page 4 Reference table with select items highlighted, page 5 Reference table with select items highlighted, page 6

homework

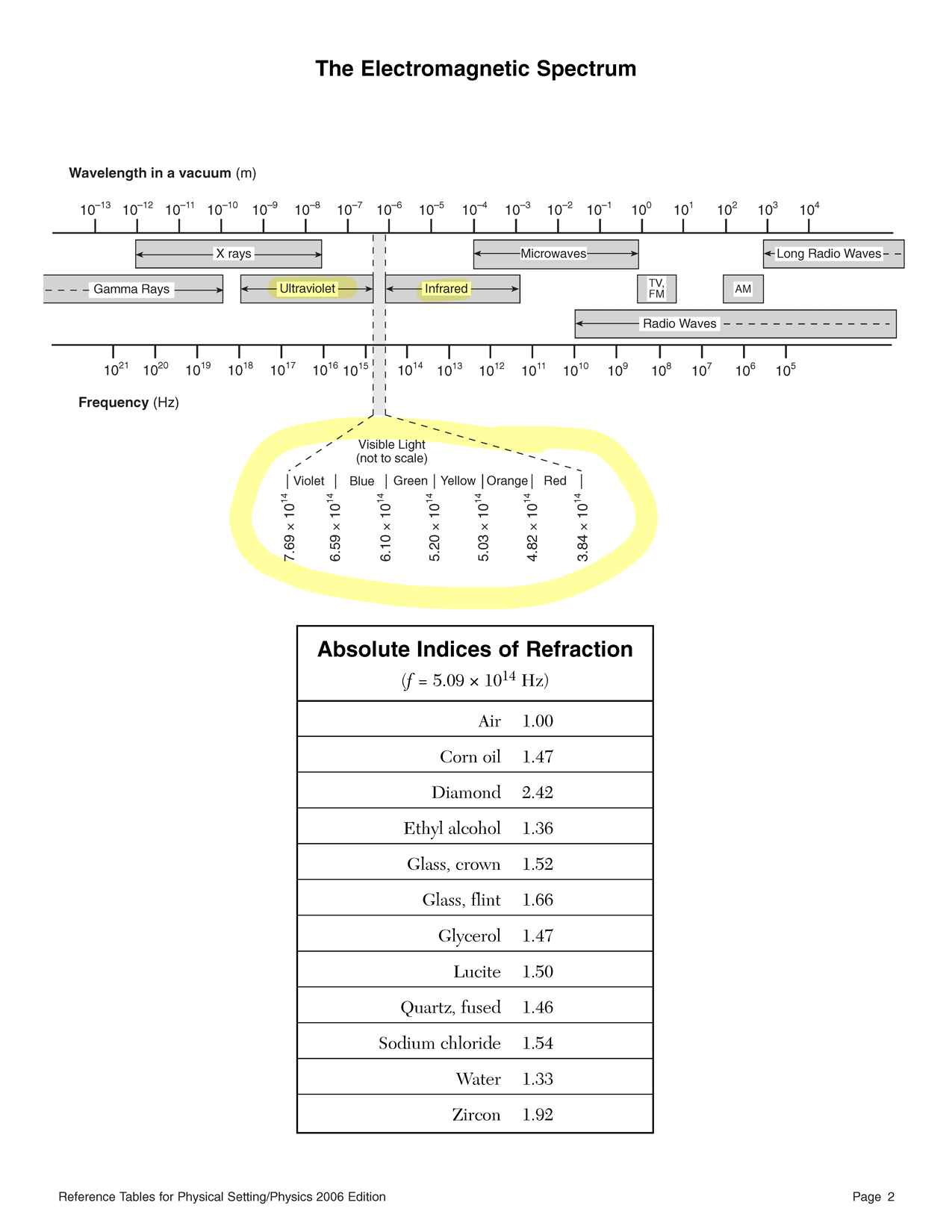
  1. Using the Reference Tables for Physical Setting/PHYSICS, determine the color of the 9 different light waves below with the following characteristics:
    1. A frequency of…
      1. 4.30 × 1014 Hz
      2. 5.63 × 1014 Hz
      3. 6.34 × 1014 Hz
    2. A wavelength of…
      1. 4.21 × 10−7 m
      2. 4.73 × 10−7 m
      3. 5.87 × 10−7 m
    3. A period of…
      1. 1.78 × 10−15 s
      2. 1.96 × 10−15 s
      3. 2.03 × 10−15 s

    The State University of New York's Reference Tables for Physical Setting/PHYSICS identify colors by frequency on a chart sorted by wavelength. Since frequency and wavelength are inversely proportional, you have to read this chart carefully.

    The top half of page 2 of the Regents Reference Tables for Physics

    1. Just looking at the frequency ranges tells us that…

      4.30 × 1014 Hz is red because it's between 3.84 × 1014 Hz and 4.82 × 1014 Hz.

      5.63 × 1014 Hz is green because it's between 5.20 × 1014 Hz and 6.10 × 1014 Hz.

      6.34 × 1014 Hz is blue because it's between 6.10 × 1014 Hz and 6.59 × 1014 Hz.

    2. Use the wavelengths given to compute the frequencies.

      f =  c
      λ
      		 ⇐  c = fλ

      Compute, then find the color in the chart.

      f =  3.00 × 108 m/s
      4.21 × 10−7 m

      f = 7.12 × 1014 Hz
      violet

      f =  3.00 × 108 m/s
      4.73 × 10−7 m

      f = 6.34 × 1014 Hz
      blue

      f =  3.00 × 108 m/s
      5.87 × 10−7 m

      f = 5.11 × 1014 Hz
      yellow

    3. Period and frequency are reciprocals.

      f =  1
      T

      Invert, then find the color in the chart.

      f =  1
      1.78 × 10−15 s

      f = 5.63 × 1014 Hz
      green

      f =  1
      1.96 × 10−15 s

      f = 5.11 × 1014 Hz
      yellow

      f =  1
      2.03 × 10−15 s

      f = 4.92 × 1014 Hz
      orange

  2. Some cars with autonomous driving capabilities use lidar to determine the distance to objects around them using pulses of laser light. The word lidar is an acronym of light detection and ranging and was intended to mimic the words radar (radio detection and ranging) and sonar (sound navigation and ranging). A detector near the laser measures the time between when a pulse was sent out and when a reflection was received back. Some systems also compare the wavelength of the reflected laser light to the wavelength transmitted. Optical data for one particular lidar system are given in the table below.
    Automotive lidar system Source: Banner Engineering
    characteristic value
    wavelength 905 nm
    pulse duration 3 ns
    pulse power 8 W
    laser class 1 EN 60825-1
    beam divergence 0.12°
    1. What type of electromagnetic radiation does this laser emit?
    2. What is the energy in one pulse of this laser?
    3. If the time of flight for one pulse to hit an object and return is 40 ns, how far away is the object from the car?
    4. If the reflected laser light has a wavelength of 904.99994 nm, what additional information does this tell you about the distance between the object and the car?

    Refer to this chart to answer part a.

    The top half of page 2 of the Regents Reference Tables for Physics

    Recall that…

    1 nm = 1 nanometer = 10−9 m
    1 ns = 1 nanosecond = 10−9 s
    1 mW = 1 milliwatt = 10−3 W
    1 THz = 1 terahertz = 1012 Hz

    1. Visible light is typically described as ranging from 700 nm (dark red) to 400 nm (dark violet). 905 nm is significantly longer than 700 nm so this lidar uses infrared. If you prefer to think in terms of frequency, visible light ranges from 400 THz (dark red) to 800 THz (dark violet). 905 nm corresponds to 332 THz which is lower than 400 THz.

      f =  c
      λ
      		 ⇐  c = fλ
      f =  3.00 × 108 m/s
      905 × 10−9 m

      f = 3.32 × 1014 Hz

    2. Determine energy from power and time.

      W = Pt  ⇐ 
      P =  W
      t

      W = (8 W)(3 × 10−9 s)

      W = 2.4 × 10−8 J or 24 nJ

    3. Determine distance from time and the speed of light. The time it takes the laser pulse to reach the object (20 ns) is half the time of flight (40 ns).

      ∆s = c∆t  ⇐ 
      c =  ∆s
      ∆t

      ∆s = (3.00 × 108 m/s)(20 × 10−9 s)

      ∆s = 6.0 m

    4. The wavelength of the reflected light (904.99994 nm) is shorter than the emitted light (905 nm). A shortened wavelength means the objects are moving toward one another. Therefore the distance is decreasing. This is an example of the Doppler effect.